Schreiber Cyclification of Orbifolds

An article that we have written:

---

• Hisham Sati$\;$and$\;$ Urs Schreiber

  
  

  Cyclification of Orbifolds

  
  

  Comm. Math. Phys. 405 67 (2024)

  doi:10.1007/s00220-023-04929-w

  
  

  download:

  • pdf

  • arXiv:2212.13836

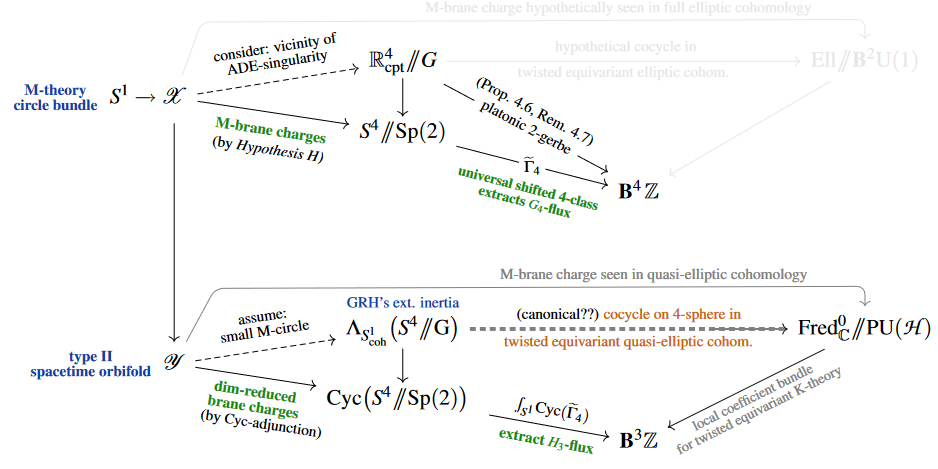
Abstract. Inertia orbifolds homotopy-quotiented by rotation of geometric loops play a fundamental role not only in ordinary cyclic cohomology, but more recently in constructions of equivariant quasi-elliptic cohomology and generally of transchromatic characters on generalized cohomology theories. Nevertheless, existing discussion of such cyclified stacks has been relying on ad-hoc component presentations with intransparent and unverified stacky homotopy type.

Following our previous formulation of transgression of cohomological charges (“double dimensional reduction”), we explain how cyclification of $\infty$-stacks is a fundamental and elementary base change construction over moduli stacks in cohesive higher topos theory (cohesive homotopy type theory). We prove that Ganter-Huan's extended inertia groupoid used to define equivariant quasi-elliptic cohomology is indeed a model for this intrinsically defined cyclification of orbifolds, and we show that cyclification implements transgression in group cohomology in general, and hence in particular the transgression of degree-4 twists of equivariant quasi-elliptic cohomology to degree-3 twists of orbifold K-theory on the cyclified orbifold.

As an application, we show that the universal shifted integral 4-class of equivariant 4-Cohomotopy theory on ADE-orbifolds induces the Platonic 4-twist of ADE-equivariant quasi-elliptic cohomology; and we close by explaining how this should relate to elliptic genera of the M5-brane, under our previously formulated Hypothesis H.

---

Related articles:

• T-Duality from super Lie n-algebra cocycles for super p-branes

  ATMP 22 5 (2018)

• Gauge enhancement of super M-branes via parametrized stable homotopy theory

  Comm. Math. Phys. 371 (2019) 197–265

Related talks:

• Cyclic loop spaces via higher topos theory in high energy physics,

  talk at: Loop spaces and Higher categories,

  HUST & SCUT (2-3 Dec 2022)

• Introduction to Higher Supergeometry

  at Higher Structures in M-Theory 2018

  Durham, Aug 2018

• Super topological T-Duality

  at Conf. on Duality in Homotopy theory

  Regensburg, April 2017

• Super Lie $n$-algebra of Super $p$-branes

  at Fields, Strings, and Geometry Seminar

  Surrey, Dec 2016